8.1树的概念
树(tree)是n(n>=0)个节点的有限集合T,它满足两个条件:
1)有且仅有一个特定的称为根(root)的节点;
2)其余的节点可以分为m(m>=0)个互不相交的有限结合T1、T2、…、Tm,其中每一个集合又是一棵树,并成为其根的子数(Subtree)。
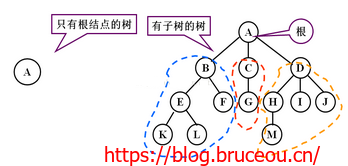
树的逻辑结构:树中任何节点都可以有零个或多个直接后继节点(子节点),但至多只有一个直接前驱节点(父节点),根节点没有前驱节点,叶节点没有后继节点。
度数:一个节点的子树的个数称为该节点的度数,一棵树的度数是指该树中节点的最大度数;
层数:节点的层数等于父节点的层数加一,根节点的层数定义为一;
深度:树中节点层数的最大值称为该树的高度或深度;
8.2二叉树
二叉树(Binary)是n(n>=0)个节点的有限集合,它或者是空集(n=0),或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树;二叉树是有序树。
二叉树的性质:
满二叉树:深度为k(k>=1)时2ek-1个节点的二叉树;
完全二叉树:1)只有最下面两层有度数小于2的节点;2)最下面一层的叶节点集中在最左边的若干位置上;
满二叉树是完全二叉树的一个特例。
1、二叉树的顺序存储结构
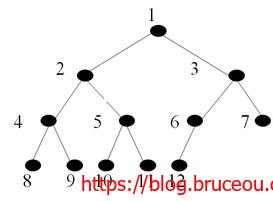
完全二叉树节点的编号方法是从上到下,从左到右,根节点为1号节点。设完全二叉树的节点数为n,某节点编号为i :
1)当i > 1(不是根节点)时,有父节点,其父节点编号为i / 2;
2)当2 i <= n 时,有左子树,其编号为2 i,否则没有左子树,本身是叶节点;
3)当2 i + 1 < = n时,有右子树,其编号为2 i + 1,否则没有右子树;
如何存储:
有n个节点的完全二叉树可以用有 n + 1 个元素的数组进行存储,节点号和数组下标一一对应,下标为零的元素不用。
利用以上特性,可以用下标获得节点的逻辑关系。不完全二叉树通过添加虚节点构成完全二叉树,然后用数组存储,这要浪费一些存储空间。
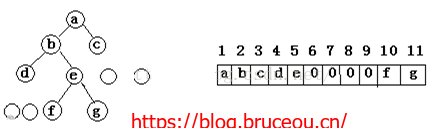
通过添加非字母字符,构成完全二叉树。
2、二叉树的链式存储
1)链式存储结构:
typedef int data_t;
typedef struct node_t //定义二叉树节点的内部结构
{
data_t data;
struct node_t *lchild,*rchild; //指向左孩子和右孩子的指针;
}bitree_t;
bitree_t *root; //定义指向二叉树的指针 2)链式二叉树的创建
链式二叉树的创建要借助顺序存储,比如下面这个二叉树。
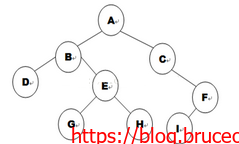
我们需要通过添加虚节点使其成为一个完全二叉树,并用大小为n+1的数组来表示,如下
data_t a[] = {0,'a','b','c','d','e',0,'f',0,0,'g','h',0,0,'i'}; 因为节点号与数组下表是一一对应的,所以我们可以通过这个数组创建一个链式二叉树
利用递归创建一个二叉树:
data_t a[] = {0,'a','b','c','d','e',0,'f',0,0,'g','h',0,0,'i'};
bitree_t *CreateBitree(int i, data_t a[], int n)
{
bitree_t *root;
int j;
root = (bitree_t *)malloc(sizeof(bitree_t));
root->data = a[i];
j = 2 * i;
if(j <= n && a[j] != '0')
{
root->lchild = CreateBitree(j, a, n); //创建
}
else
{
root->lchild = NULL;
}
j = 2 * i + 1;
if(j <= n && a[j] != '0')
{
root->rchild = CreateBitree(j, a, n);
}
else
{
root->rchild = NULL;
}
return root;
} 它的遍历顺序:

递归不论是在我们创建二叉树还是遍历二叉树都起到了很大的作用,至于递归,大家可以通过函数栈来理解,函数在执行到 root->lchild = CreateBitree(j, a, n); 这一步时,会再次调用CreateBitree()函数,这样会在栈区开辟一块空间,知道遇到终止条件才会返回,即这片内存区域会被释放,函数执行向上回收,直至该二叉树被创建。
3、二叉树的遍历
遍历:沿某条搜索路径周游二叉树,对树中的每一个节点访问一次且仅访问一次。
由于二叉树的递归性质,遍历算法也是递归的。三种基本的遍历算法如下:
1)先序遍历:先访问树根,再访问左子树,最后访问右子树;
2)中序遍历:先访问左子树,再访问树根,最后访问右子树;
3)后序遍历:先访问左子树,再访问右子树,最后访问树根;
先序遍历算法:
void PREORDER(bitree_t *r)
{
if(r == NULL)
return;
printf("%c ",r->data);
PREORDER(r->lchild);
PREORDER(r->rchild);
} 中序遍历算法:
void INORDER(bitree_t *r)
{
if(r == NULL)
return;
INORDER(r->lchild);
printf("%c ",r->data);
INORDER(r->rchild);
} 后序遍历算法:
void POSTORDER(bitree_t *r)
{
if(r == NULL)
return;
POSTORDER(r->lchild);
POSTORDER(r->rchild);
printf("%c ",r->data);
} 我们可以把程序整合一下,写个测试程序:
int main()
{
bitree_t *tree;
printf("Begin creating the tree!\n");
tree = CreateBitree(1,a,sizeof(a)/sizeof(data_t) - 1);
printf("Finish!\n");
printf("Preorder traversal:\n");
PREORDER(tree);
printf("\nInorder traversal:\n");
INORDER(tree);
printf("\nPostorder traversal:\n");
POSTORDER(tree);
printf("\n");
return 0;
} 执行结果如下:
$ ./bitree
Begin creating the tree!
Finish!
Preorder traversal:
a b d e g h c f i
Inorder traversal:
d b g e h a c i f
Postorder traversal:
d g h e b i f c a
资源获取方法
1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料提取码

